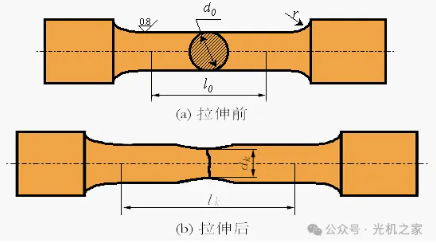
The tensile test of strength is mainly used to determine the ability of metal materials to resist damage during the stretching process, and is one of the important indicators for evaluating the mechanical properties of materials.
1. Tensile test
The tensile test is based on the basic principles of material mechanics. By applying a tensile load to the material sample under certain conditions, it causes tensile deformation until the sample breaks. During the test, the deformation of the experimental sample under different loads and the maximum load when the sample breaks are recorded, so as to calculate the yield strength, tensile strength and other performance indicators of the material.
Stress σ = F/A
σ is the tensile strength (MPa)
F is the tensile load (N)
A is the cross-sectional area of the specimen
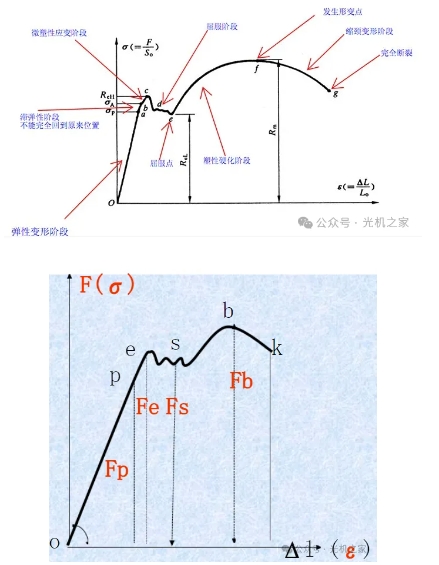
2. Tensile curve
Analysis of several stages of the stretching process:
a. In the OP stage with a small load, the elongation is in a linear relationship with the load, and Fp is the maximum load to maintain the straight line.
b. After the load exceeds Fp, the tensile curve begins to take a non-linear relationship. The sample enters the initial deformation stage, and the load is removed, and the sample can return to its original state and elastically deform.
c. After the load exceeds Fe, the load is removed, part of the deformation is restored, and part of the residual deformation is retained, which is called plastic deformation. Fe is called the elastic limit.
d. When the load increases further, the tensile curve shows sawtooth. When the load does not increase or decrease, the phenomenon of continuous elongation of the experimental sample is called yielding. After yielding, the sample begins to undergo obvious plastic deformation.
e. After yielding, the sample shows an increase in deformation resistance, work hardening and deformation strengthening. When the load reaches Fb, the same part of the sample shrinks sharply. Fb is the strength limit.
f. The shrinkage phenomenon leads to a decrease in the bearing capacity of the sample. When the load reaches Fk, the sample breaks. This is called the fracture load.
Yield Strength
Yield strength is the maximum stress value that a metal material can withstand from the beginning of plastic deformation to complete fracture when subjected to external force. This value marks the critical point where the material transitions from the elastic deformation stage to the plastic deformation stage.
Classification
Upper yield strength: refers to the maximum stress of the sample before the force drops for the first time when yielding occurs.
Lower yield strength: refers to the minimum stress in the yield stage when the initial transient effect is ignored. Since the value of the lower yield point is relatively stable, it is usually used as an indicator of material resistance, called yield point or yield strength.
Calculation formula
For upper yield strength: R = F / Sₒ, where F is the maximum force before the force drops for the first time in the yield stage, and Sₒ is the original cross-sectional area of the sample.
For lower yield strength: R = F / Sₒ, where F is the minimum force F ignoring the initial transient effect, and Sₒ is the original cross-sectional area of the sample.
Unit
The unit of yield strength is usually MPa (megapascal) or N/mm² (Newton per square millimeter).
Example
Take low carbon steel as an example, its yield limit is usually 207MPa. When subjected to an external force greater than this limit, low carbon steel will produce permanent deformation and cannot be restored; when subjected to an external force less than this limit, low carbon steel can return to its original state.
Yield strength is one of the important indicators for evaluating the mechanical properties of metal materials. It reflects the ability of materials to resist plastic deformation when subjected to external forces.
Tensile strength
Tensile strength is the ability of a material to resist damage under tensile load, which is specifically expressed as the maximum stress value that the material can withstand during the tensile process. When the tensile stress on the material exceeds its tensile strength, the material will undergo plastic deformation or fracture.
Calculation formula
The calculation formula for tensile strength (σt) is:
σt = F / A
Where F is the maximum tensile force (Newton, N) that the specimen can withstand before breaking, and A is the original cross-sectional area of the specimen (square millimeter, mm²).
Unit
The unit of tensile strength is usually MPa (megapascal) or N/mm² (Newton per square millimeter). 1 MPa is equal to 1,000,000 Newtons per square meter, which is also equal to 1 N/mm².
Influencing factors
Tensile strength is affected by many factors, including the chemical composition, microstructure, heat treatment process, processing method, etc. Different materials have different tensile strengths, so in practical applications, it is necessary to select suitable materials based on the mechanical properties of the materials.
Practical application
Tensile strength is a very important parameter in the field of materials science and engineering, and is often used to evaluate the mechanical properties of materials. In terms of structural design, material selection, safety assessment, etc., tensile strength is a factor that must be considered. For example, in construction engineering, the tensile strength of steel is an important factor in determining whether it can withstand loads; in the field of aerospace, the tensile strength of lightweight and high-strength materials is the key to ensuring the safety of aircraft.
Fatigue strength:
Metal fatigue refers to the process in which materials and components gradually produce local permanent cumulative damage in one or several places under cyclic stress or cyclic strain, and cracks or sudden complete fractures occur after a certain number of cycles.
Features
Suddenness in time: Metal fatigue failure often occurs suddenly in a short period of time without obvious signs.
Locality in position: Fatigue failure usually occurs in local areas where stress is concentrated.
Sensitivity to environment and defects: Metal fatigue is very sensitive to the environment and tiny defects inside the material, which may accelerate the fatigue process.
Influencing factors
Stress amplitude: The magnitude of stress directly affects the fatigue life of the metal.
Average stress magnitude: The greater the average stress, the shorter the fatigue life of the metal.
Number of cycles: The more times the metal is under cyclic stress or strain, the more serious the accumulation of fatigue damage.
Preventive measures
Optimize material selection: Select materials with higher fatigue limits.
Reducing stress concentration: Reduce stress concentration through structural design or processing methods, such as using rounded corner transitions, increasing cross-sectional dimensions, etc.
Surface treatment: Polishing, spraying, etc. on the metal surface to reduce surface defects and improve fatigue strength.
Inspection and maintenance: Regularly inspect metal components to promptly detect and repair defects such as cracks; maintain parts prone to fatigue, such as replacing worn parts and reinforcing weak links.
Metal fatigue is a common metal failure mode, which is characterized by suddenness, locality and sensitivity to the environment. Stress amplitude, average stress magnitude and number of cycles are the main factors affecting metal fatigue.
S-N curve: describes the fatigue life of materials under different stress levels, where S represents stress and N represents the number of stress cycles.
Fatigue strength coefficient formula:
(Kf = Ka \cdot Kb \cdot Kc \cdot Kd \cdot Ke)
Where (Ka) is the load factor, (Kb) is the size factor, (Kc) is the temperature factor, (Kd) is the surface quality factor, and (Ke) is the reliability factor.
S-N curve mathematical expression:
(\sigma^m N = C)
Where (\sigma) is stress, N is the number of stress cycles, and m and C are material constants.
Calculation steps
Determine the material constants:
Determine the values of m and C through experiments or by referring to relevant literature.
Determine the stress concentration factor: Consider the actual shape and size of the part, as well as the stress concentration caused by fillets, keyways, etc., to determine the stress concentration factor K. Calculate fatigue strength: According to the S-N curve and stress concentration factor, combined with the design life and working stress level of the part, calculate the fatigue strength.
2. Plasticity:
Plasticity refers to the property of a material that, when subjected to external force, produces permanent deformation without breaking when the external force exceeds its elastic limit. This deformation is irreversible, and the material will not return to its original shape even if the external force is removed.
Plasticity index and its calculation formula
Elongation (δ)
Definition: Elongation is the percentage of the total deformation of the gauge section after the specimen is tensile fractured to the original gauge length.
Formula: δ = (L1 – L0) / L0 × 100%
Where L0 is the original gauge length of the specimen;
L1 is the gauge length after the specimen is broken.
Segmental reduction (Ψ)
Definition: The segmental reduction is the percentage of the maximum reduction in the cross-sectional area at the necking point after the specimen is broken to the original cross-sectional area.
Formula: Ψ = (F0 – F1) / F0 × 100%
Where F0 is the original cross-sectional area of the specimen;
F1 is the cross-sectional area at the necking point after the specimen is broken.
3. Hardness
Metal hardness is a mechanical property index to measure the hardness of metal materials. It indicates the ability to resist deformation in the local volume on the metal surface.
Classification and representation of metal hardness
Metal hardness has a variety of classification and representation methods according to different test methods. Mainly include the following:
Brinell hardness (HB):
Scope of application: Generally used when the material is softer, such as non-ferrous metals, steel before heat treatment or after annealing.
Test principle: With a certain size of test load, a hardened steel ball or carbide ball of a certain diameter is pressed into the surface of the metal to be tested, and the load is unloaded after a specified time, and the diameter of the indentation on the surface to be tested is measured.
Calculation formula: The Brinell hardness value is the quotient obtained by dividing the load by the spherical surface area of the indentation.
Rockwell hardness (HR):
Scope of application: Generally used for materials with higher hardness, such as hardness after heat treatment.
Test principle: Similar to Brinell hardness, but using different probes (diamond) and different calculation methods.
Types: Depending on the application, there are HRC (for high hardness materials), HRA, HRB and other types.
Vickers hardness (HV):
Scope of application: Suitable for microscope analysis.
Test principle: Press the material surface with a load of less than 120kg and a diamond square cone indenter with a vertex angle of 136°, and divide the surface area of the material indentation pit by the load value to get the Vickers hardness value.
Leeb hardness (HL):
Features: Portable hardness tester, easy to measure.
Test principle: Use the bounce generated by the impact ball head after impacting the hardness surface, and calculate the hardness by the ratio of the rebound speed of the punch at 1mm from the sample surface to the impact speed.
Post time: Sep-25-2024